Triangles ⇒⇒ Exercise 7.2

Question 1

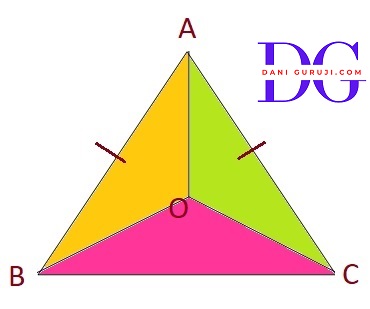
In an isosceles triangle ABC, with AB = AC, the bisectors of $\angle $B and $\angle $C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects $\angle $A

Solution :

It is given information that in triangle ABC is isosceles with AB = AC .

(i): Proof that OB = OC

Consider the triangles Δ ABC

⇒ AB = AC

( Given in the problem. )

⇒ $\angle $B = $\angle $C

( the angles opposite to these equal sides are also equal. )

Dividing both sides of equation by 2, we get :

⇒ ${ 1 \over 2} \angle $ B = $ { 1 \over 2} \angle $ C

Since BO and CO are the bisectors of $\angle $B and $\angle $C respectively, we have:

⇒ $\angle $ OBC = ${ 1 \over 2} \angle $ B

⇒ $\angle $ OCB = ${ 1 \over 2} \angle $ C

∴ $\angle $OBC = $\angle $OCB.

( As ${ 1 \over 2} \angle $ B = $ { 1 \over 2} \angle $ C. Angle bisectors)

Consider the triangles Δ OBC

OB = OC

( Since $\angle $OBC = $\angle $OCB, the sides opposite to these equal angles must also be equal. The side opposite to $\angle $OBC is OC, and the side opposite to $\angle $OCB is OB. )

(ii) AO bisects $\angle $A

Consider the triangles Δ ABO and Δ ACO

⇒ AB = AC

( Given in the problem. )

⇒ OB = OC

( Proved in part i )

⇒ AO = AO

( This is a common side for both triangles. )

∴ ΔABO $\cong$ ΔACO

( by the SSS congruence rule. )

Since the triangles are congruent, We know that, Corresponding parts of congruent triangles are equal. Therefore,

⇒ $\angle $BAO = $\angle $CAO

∴ AO bisects $\angle $A

Question 2

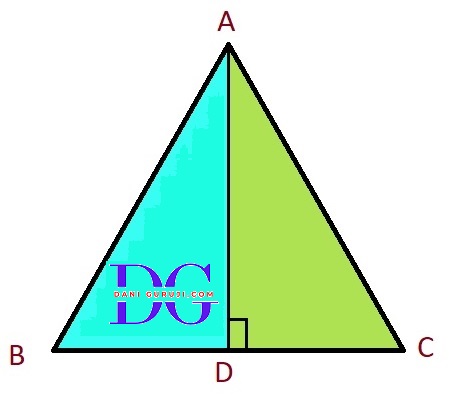
In ΔABC, AD is the perpendicular bisector of BC (see Fig). Show that ΔABC is an isosceles triangle in which AB = AC.

Solution :

From given figure, It is given that

AD is the perpendicular bisector of BC. This means that

$\angle $ADB = $\angle $ADC = 90°

AD bisects BC, so BD = CD

Consider the triangles Δ ABD and Δ ACD

⇒ BD = CD

( Given, since AD is the bisector of BC. )

⇒ $\angle $ADB = $\angle $ADC

( Both are 90°. )

⇒ AD = AD

( Common side to both triangles. )

∴ ΔABD $\cong$ ΔACD

( by the SAS congruence rule. )

Since the two triangles are congruent, their corresponding parts must be equal

AB = AC. (By C.P.C.T.)

By definition, a triangle with two equal sides is an isosceles triangle. Since we have shown that

AB = AC, △ABC is an isosceles triangle.

Question 3

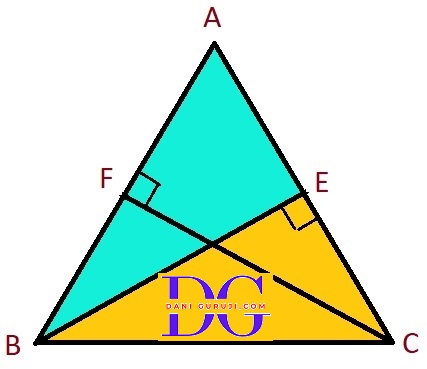
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively see Fig. Show that these altitudes are equal.

Solution :

From given figure, It is given that

△ABC is an isosceles triangle with AB = AC

BE is an altitude to side AC, which means = $\angle $BEC = 90°

CF is an altitude to side AB, which means = $\angle $CFB = 90°

Consider the triangles Δ EBC and Δ FCB

⇒ BC = CB

( Common side to both triangles. )

⇒ $\angle $BEC = $\angle $CFB

( Both are 90°. )

⇒ $\angle $EBC = $\angle $FCB

( Since AB = AC, the angles opposite to these sides are equal, so. $\angle $ABC = $\angle $ACB. This means $\angle $EBC = $\angle $FCB )

∴ ΔEBC $\cong$ ΔFCB

( by the AAS congruence rule. )

Since the two triangles are congruent, their corresponding parts must be equal

BE = CF. (By C.P.C.T.)

Question 4

ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Show that
(i)ΔABE $\cong$ Δ ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle

Solution :

From given figure, It is given that

Altitudes, BE = CF,

CF is an altitude to side AB, which means = $\angle $AFC = 90°

BE is an altitude to side AC, which means = $\angle $ AEB = 90°

Consider the triangles ΔABE and Δ ACF

⇒ BE = CF

( Given that the altitudes are equal. )

⇒ $\angle $AFC = $\angle $ AEB

( Both are 90°. )

⇒ $\angle $BAE = $\angle $CAF

( they are the same angle, $\angle $A )

∴ ΔABE $\cong$ Δ ACF

( by the AAS congruence rule. )

Since the two triangles are congruent, their corresponding parts must be equal

AB = AC (By C.P.C.T.)

A triangle with two equal sides is defined as an isosceles triangle.

Since we have shown that AB = AC, it follows that △ABC is an isosceles triangle.

Question 5

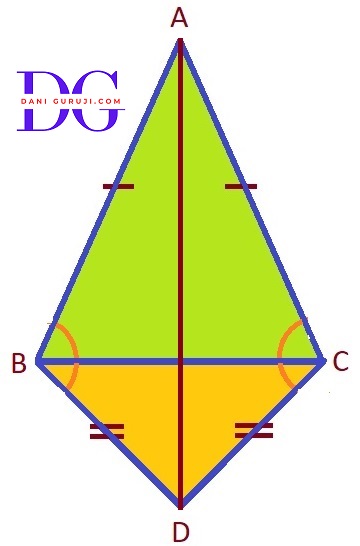
ABC and DBC are two isosceles triangles on the same base BC (see fig.). Show that
$\angle $ABD = $\angle $ACD

Solution :

Let us join AD

Consider the triangles ΔABD and Δ ACD,

⇒ AB = AC

( Given that △ABC is an isosceles triangle with base BC. )

⇒ DB = DC

( Given that △DBC is an isosceles triangle with base BC. )

⇒ AD = AD

( This is a common side for both triangles )

∴ ΔABD $\cong$ Δ ACD

( by the SSS congruence rule. )

Since the two triangles are congruent, their corresponding parts must be equal

$\angle $ ABD = $\angle $ACD. (By C.P.C.T.)

Question 6

ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see fig.). Show that $\angle $BCD is a right angle.

Solution :

From given figure, It is given that

△ABC is an isosceles triangle with AB = AC

Side BA is extended to point D

AD = AB

Consider the triangles ΔABC

⇒ AB = AC

( Given that △ABC is an isosceles triangle with base BC. )

⇒ $\angle $ACB = $\angle $ABC -------( equation 1)

( the angles opposite to these equal sides must also be equal. )

Consider the triangles ΔACD,

⇒ AD = AB

( Given in problem statement )

We also know that AB = AC

Therefore, by the transitive property of equality,

AD = AC.

This means that △ACD is also an isosceles triangle with AD = AC

$\angle $ACD = $\angle $ADC -------( equation 2)

( the angles opposite to these equal sides must also be equal. )

Apply the Angle Sum Property of a Triangle
Consider the triangles ΔBCD

⇒ $\angle $BCD + $\angle $CDB + $\angle $CBD = 180°.

( The sum of the angles in any triangle is 180°. )

We also know that
$\angle $BCD = $\angle $ ACB + $\angle $ACD -------( equation 3)

And, $\angle $CDB = $\angle $ADC

∴ $\angle $ADC = $\angle $ACD

( from equation 2 )

And, $\angle $CBD = $\angle $ABC

∴ $\angle $ABC = $\angle $ACB

( from equation 1 )

Substitute these values into the angle sum equation:

( $\angle $ ACB + $\angle $ACD )+ $\angle $ACD + $\angle $ACB = 180°

$\angle $BCD + $\angle $BCD = 180°

( from equation 3 )

2 $\angle $BCD = $ { 180° }$

$\angle $BCD = $ { 180° \over 2}$

$\angle $BCD = $ { 90° }$

Therefore, $\angle $BCD is a right angle.

Question 7

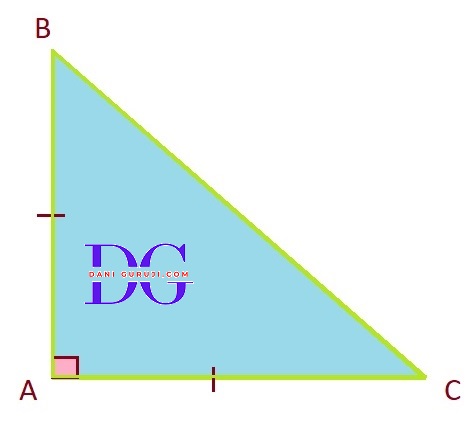
ABC is a right angled triangle in which $\angle $A = 90° and AB = AC. Find $\angle $B and $\angle $C.

Solution :

It is given that

△ABC is an isosceles triangle with AB = AC

$\angle $A = 90°

Consider the triangles ΔABC

Apply the Angle Sum Property of a Triangle

⇒ $\angle $A + $\angle $B + $\angle $C = 180°.

( The sum of the angles in any triangle is 180°. )

⇒ 90° + $\angle $B + $\angle $C = 180°.

⇒ $\angle $B + $\angle $C = 180° - 90°

⇒ $\angle $B + $\angle $C = 90°

Since we know that $\angle $B = $\angle $C

( Since the triangle is isosceles with AB = AC, the angles opposite to these equal sides must also be equal. )

Substitute these values into the angle sum equation:

90° + $\angle $B + $\angle $B = 180°.

2 $\angle $B = $ { 180° - 90° }$

$\angle $B = $ { 90° \over 2}$

$\angle $B = $ { 45° }$

Since $\angle $B = $\angle $C, we also have:$\angle $C = 45°

Thus, in the given triangle $\angle $B = 45° , $\angle $C = 45°

Question 8

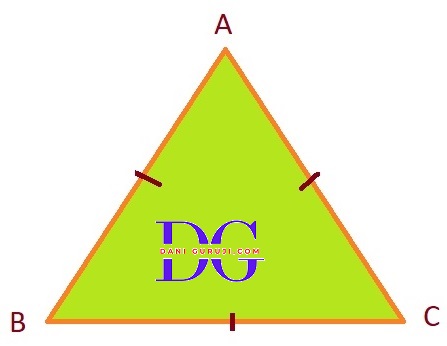
Show that the angles of an equilateral triangle are 60° each.

Solution :

Let's consider a triangle, △ABC, where AB = BC = CA.

Since we know that AB = BC

( the angles opposite to these sides must be equal.)

⇒ $\angle $A = $\angle $C

Since we know that BC = CA

( the angles opposite to these sides must be equal.)

⇒ $\angle $A = $\angle $B

From the above, we can conclude that all three angles are equal:

$\angle $A = $\angle $B = $\angle $C

Apply the Angle Sum Property of a Triangle

⇒ $\angle $A + $\angle $B + $\angle $C = 180°.

( The sum of the angles in any triangle is 180°. )

⇒ 3$\angle $A = 180°

( Since all three angles are equal, we can substitute $\angle $A for $\angle $B and $\angle $C: )

⇒ $\angle $A = $ { 180° \over 3}$

⇒ $\angle $A = $ { 60° }$

Since $\angle $A = $\angle $B = $\angle $C, all three angles are 60° each.