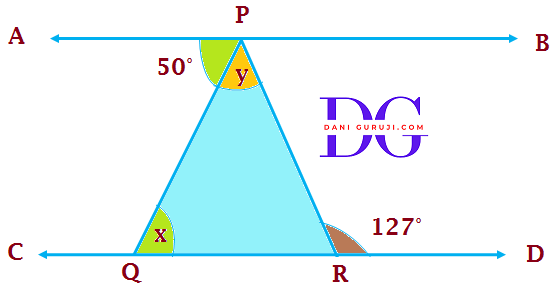
KEY Concept For Chpt. 6.2 Theorems on Lines and angles
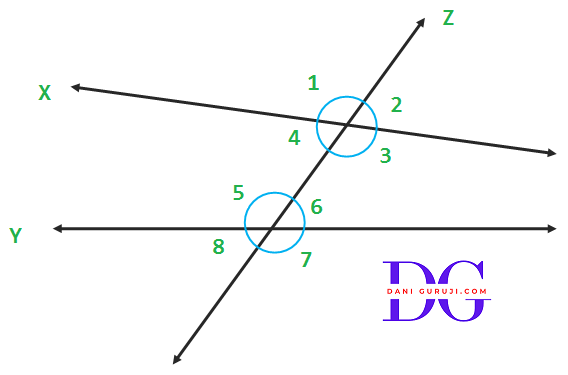
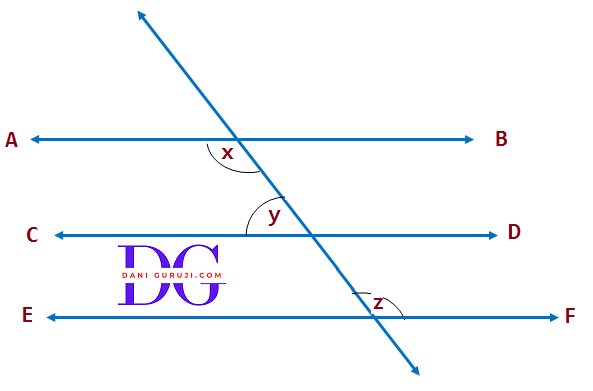
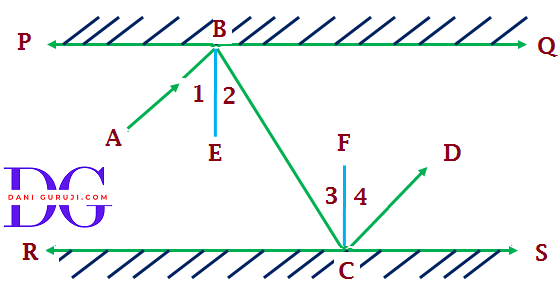
Transversal Line
If a line 'Z' passes through two distinct lines ('X' and 'Y') and intersects them at distant points then this line 'Z' is called Transversal Line.
Exterior Angles
In above figure Exterior angles are $ \angle $ 1, $ \angle $ 2 and $ \angle $ 7 and $ \angle $ 8 .
Interior Angles
In above figure Interior Angles are $ \angle $ 3, $ \angle $ 4 and $ \angle $ 5 and $ \angle $ 6 .
When a transversal intersects two lines, pairs of angles formed
1. Corresponding Angles :
$ \angle $ 1 and $ \angle $ 5
$ \angle $ 2 and $ \angle $ 6
$ \angle $ 4 and $ \angle $ 8
$ \angle $ 3 and $ \angle $ 7
2. Alternate Exterior Angles:
$ \angle $ 1 and $ \angle $ 7
$ \angle $ 2 and $ \angle $ 8
3. Alternate Interior Angles :
$ \angle $ 3 and $ \angle $ 5
$ \angle $ 4 and $ \angle $ 6
4. Interior Angles on the same side of the transversal :
$ \angle $ 3 and $ \angle $ 6
$ \angle $ 4 and $ \angle $ 5
Theorem 6.4
If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
Theorem 6.5
If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.
Theorem 6.6
If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
Theorem 6.7
If a transversal intersects two lines such that a pair of interior angles on the same side of transversal is supplementary, then the two lines are parallel.
Theorem 6.8
Lines which are parallel to the same line are parallel to each other.