State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
Solution :
(i)True .
The set of real numbers is comprised of both rational numbers (numbers that can be written as a fraction, like (1/2) and irrational numbers (numbers that cannot be written as a fraction, like ${ \sqrt 5}$ or π).
Therefore, by definition, all irrational numbers are a subset of the real numbers.
State whether the following statements are true or false. Justify your answers.
(ii) Every point on the number line is of the form √m , where m is a Natural number
Solution :
(ii) False .
The number line includes negative numbers (e.g., -2), which cannot be the square root of a natural number. The square root of a natural number is always non-negative.
The square root of a natural number, such as ${ \sqrt 2}$ , corresponds to a point on the number line. However, not all points can be represented this way. For example, ${ \sqrt 1.5}$ is a real number, but 1.5 is not a natural number..
State whether the following statements are true or false. Justify your answers.
(iii) Every real number is an irrational number.
Solution :
(iii) False .
Because , All Rational Numbers and Irrational Numbers together are called Real Number.
Therefore every Irrational number is a Real Number, but every Real Number cannot be an Irrational number.
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Solution :
No, the square roots of all positive integers are not irrational. The square root of a positive integer is a rational number if the integer is a perfect square.
A perfect square is an integer that results from squaring another integer.
Here is an example: : √49 = 7
If we take a positive integer 49 and its square root is √49 = 7 , which is a rational number.
Because 7 can be written in the form of ${ p \over q} = { 7 \over 1} $.
Where both the numerator and the denominator are integers and the denominator is not zero.
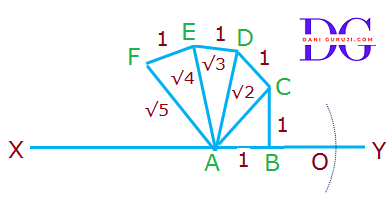
Show how √5 can be represented on the number line.
Solution :
For the square root spiral follow the given steps to show √5 on a number line:
Step: 1 – Draw a number line XY .
Step: 2 – Take AB of length 1 unit
Step: 3 – Draw a perpendicular BC of length 1 unit on point B.
Step: 4 – Now, Join point A and point C forming a line AC.
Step: 5 – This AC will be equal to √2 .This can be easily found using Pythagoras Theorem in right triangle ABC
Step: 6 – Now, Draw a perpendicular CD of length 1 unit at point C and join points A and D.
Step: 7 – Here, AD represents a line of length √3 units
Step: 8 – Now, Draw a perpendicular DE of length 1 unit at point D and join points A and E.
Step: 9 – Here, AE represents a line of length √4 units i.e. equal to 2 unit.
Step: 10 – Now, Draw a perpendicular EF of length 1 unit at point E and join points A and F.
Step: 11 – Here, AF represents a line of length √5 units .
Step: 12 – Taking AF as a radius and A as the center, construct an arc touching the number line.
Step: 13 – The number line gets intersected by the arc at a point O which is at √5 distance from 0, as it is a radius of the circle with center A
Step: 14 – Thus, √5 is represented on the number line as AO
Explanation: how, AF is equal to √5
Now, in △AEF , AE = 2 unit , FE = 1 unit
and ∠AEF = 90º
Thus, according to Pythagoras theorem.
AF2 = AE2 + EF2
AF2 = 22 + 12
AF2 = 4 + 1
AF2 = 5
AF = √5
Syllabus for class 10
Advanced courses and exam preparation.
Previous Year Paper
Advanced courses and exam preparation.
Mock Test
Explore programming, data science, and AI.