Heron's Formula ⇒⇒ Exercise 10.2

Question 1

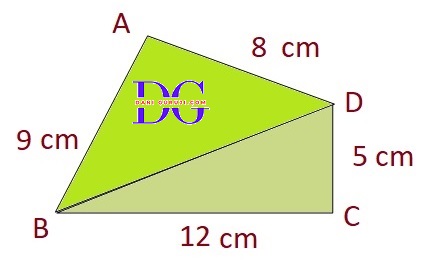
A park, in the shape of a quadrilateral ABCD, has ∠ C = 90º, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?

Solution :

A quadrilateral can be divided into triangles. Since we have a right angle at C (∠= 90º ), we can draw a diagonal line connecting points B and D. This will split the quadrilateral ABCD into two triangles:

Calculate the Area of Triangle BCD

Triangle BCD has a right angle at C.

The formula for the area of a right-angled triangle is:

Area of △BCD = $ { 1 \over 2} $ × base × height

$$⇒ { { 1 \over 2} × 12 × 5 } $$

$$⇒ { { 1 \over 2} × 60 } $$

$$⇒ { 30 } $$

Area of △BCD = 30 m²

Find the Length of the Diagonal BD

The diagonal BD is the hypotenuse of the right-angled △BCD

We can find its length using the Pythagorean theorem, :

( It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.)

$$ BD^2 = BC^2 + CD^2 $$

$$⇒ BD^2 = (12)^2 + (5)^2 $$

$$⇒ BD^2 = 144 + 25 $$

$$⇒ BD^2 = 169 m^2 $$

To find BD, take the square root of both sides

$$⇒ BD = 13 m $$

Calculate the Area of Triangle ABD

First, calculate the semi-perimeter (s) of △ABD

Semi perimeter of the signal board (s) = $$ { { a + b + c } \over 2} $$

$$ { { 9 + 8 + 13 } \over 2} $$

$$ = 15m $$

Using Heron's formula calculate the area of Triangle ABD

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{15 ( 15 - 9 ) ( 15 - 8 )( 15 - 13 )}} $$

$$⇒ {\sqrt{15 × 6 × 7 × 2 } } $$

$$⇒ {\sqrt{( 3 × 5) × ( 3 × 2) × 7 × 2 } } $$

( Taking 3 × 2 outside the square root, as a pair is present in square root )

$$⇒ 3 × 2 ×{\sqrt{5 × 7} } $$

$$⇒ 6 {\sqrt{35} } $$

$$⇒ {6 × 5.916 } $$

( Take √ 35 = 5.916 )

Area of △ABD = $ 35.496 m^2  $

Calculate the Total Area of the Quadrilateral ABCD

Total Area = Area of △BCD + Area of △ABD

Total Area = $ {30 m^2 + 35.496 } m^2 $

Total Area of the Quadrilateral ABCD = $ {65.496 } m^2 $

Question 2

Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.

Solution :

A quadrilateral can be divided into triangles. We can draw a diagonal line connecting points A and C. This will split the quadrilateral ABCD into two triangles:

Calculate the Area of Triangle ABC

First, calculate the semi-perimeter (s) of △ABC

Semi perimeter of the Triangle ABC (s) = $$ { { a + b + c } \over 2} $$

$$ { { 3 + 4 + 5 } \over 2} $$

$$ = 6cm $$

Using Heron's formula calculate the area of Triangle ABC

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{6 ( 6 - 3 ) ( 6 - 4 )( 6 - 5 )}} $$

$$⇒ {\sqrt{6 × 3 × 2 × 1 } } $$

$$⇒ {\sqrt{ 6 × 6 } } $$

( Taking 6 outside the square root, as a pair is present in square root )

$$⇒ { 6} $$

Area of △ABC = $ { 6} cm^2 $

Calculate the Area of Triangle ADC

First, calculate the semi-perimeter (s) of △ADC

Semi perimeter of the Triangle ADC (s) = $$ { { a + b + c } \over 2} $$

$$ { { 5 + 4 + 5 } \over 2} $$

$$ = 7cm $$

Using Heron's formula calculate the area of Triangle ADC

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{7 ( 7 - 5 ) ( 7 - 4 )( 7 - 5 )}} $$

$$ {\sqrt{7 × 2 × 3 × 2 }} $$

$$⇒ { 2 × { \sqrt{21}} } $$

( Taking 2 outside the square root, as a pair is present in square root )

$$⇒ {2 × 4.58 } $$

( Take √ 21 = 4.58 )

$$⇒ {9.165 } $$

Area of △ADC = $ {9.165 } cm^2 $

Calculate the Total Area of the Quadrilateral ABCD

Total Area = Area of △ABC + Area of △ADC

Total Area = $ {6 cm^2 + {9.165 } } cm^2 $

Total Area of the Quadrilateral ABCD = $ {15.165 } = 15.2 cm^2 $

Question 3

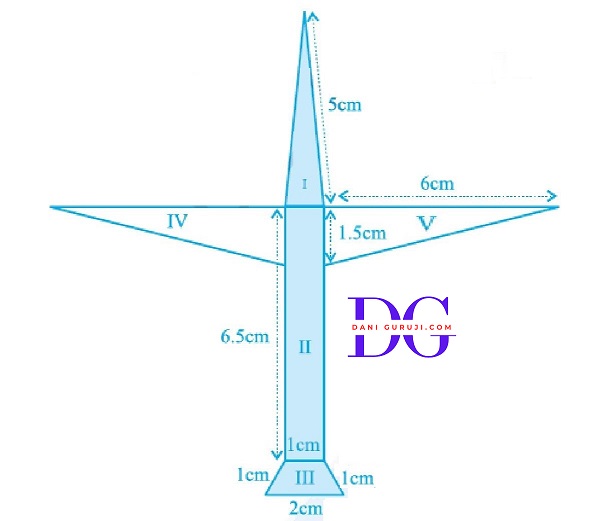
Radha made a picture of an aero plane with colored paper as shown in Fig 12.15. Find the total area of the paper used.

Solution :

We can calculate the area of polygon by dividing the polygon into triangular and quadrilateral part

Calculate Area of Part ( I ): Triangle

It is an isosceles triangle and the sides are 5 cm, 1 cm and 5 cm

Semi perimeter of the Triangle ABC (s) =

$$ { { 5 + 1 + 5 } \over 2} $$

$$ = 5.5 cm $$

Using Heron's formula calculate the area of Triangle

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{5.5 ( 5.5 - 5 ) ( 5.5 - 1 )( 5.5 - 5 )}} $$

$$⇒ {\sqrt{5.5 × 0.5 × 4.5 × 0.5 } } $$

$$⇒ 0.75 {\sqrt{ 11 } } $$

$ ⇒ 0.75 × 3.317cm^2 $

$ ⇒ 2.488cm^2 $

Area of Triangle Part ( I ) = $ 2.488 cm^2 $

Calculate Area of Part ( II ): quadrilateral

This quadrilateral is a rectangle which sides 6.5 cm and 1 cm is

Area of quadrilateral Part ( II ) = Length x Breadth

$$ { 6.5 × 1} $$

$$ = 6.5 $$

Area of quadrilateral part ( II ) = $ { 6.5 } cm^2 $

Calculate Area of Part ( III ): trapezium

This is a trapezoid with 2 sides as 1 cm each and the third side as 2 cm

Draw two lines JL and KM perpendicular to EF to divide part III into three sub-parts: Triangle JEL, Rectangle JKLM and Triangle KMF.

So, EL = MF=0.5 cm and LM = 1 cm.

In right-angled triangle JEL, height JL is calculated by Pythagoras theorem:

$$⇒ { (JE)^2 = (JL)^2 + (EL)^2 } $$

$$⇒ { (JL)^2 = (JE)^2 - (EL)^2 } $$

$$⇒ { (JL)^2 = (1)^2 - (0.5)^2 } $$

$$⇒ { JL = { \sqrt{ 1 - 0.25}} } $$

$$⇒ { JL = { \sqrt{ 0.75}} } $$

$$⇒ { JL = 0.9 cm Approx. } $$

Area of Part ( III ): trapezium =

$ { 1 \over 2} $ × (Sum of parallel sides) × distance between them

$$⇒ { {1 \over 2} × ( EF + JK ) × (JL)} $$

$$⇒ { {1 \over 2} × ( 2 + 1 ) × 0.9} $$

$$⇒ { 1.35} $$

Area of Part ( III ): trapezium = $ { 1.35} cm^2 $

Calculate the area of Part (IV) and (V):

Since Part (IV) and (V) are symmetrical, they have equal areas.

Triangles IV and V are congruent right-angled triangles with base 6 cm and height 1.5 cm

The formula for the area of a right-angled triangle is:

Area of Part (IV) △ = $ { 1 \over 2} $ × base × height

$$⇒ { { 1 \over 2} × 6 × 1.5 } $$

$$⇒ { 4.5 } cm^2 $$

Area of two triangles ( IV & V ) = $ 4.5 + 4.5 = 9cm^2 $

Calculate the total area of paper used:=

= ( 2.488 + 6.5+ 1.35 + 9 )

$ = 19.338 cm^2 $

Question 4

A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.

Solution :

Given in the question,
That the parallelogram and triangle have equal areas .

The sides of the △CDF are given as 26 cm, 28 cm and 30 cm

Calculate the Area of Triangle CDF

First, calculate the semi-perimeter (s) of △CDF

Semi perimeter of the Triangle CDF (s) = $$ { { a + b + c } \over 2} $$

$$ { { 30 + 28 + 26 } \over 2} $$

$$ = 42cm $$

Using Heron's formula calculate the area of Triangle CDF

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{42 ( 42 - 30 ) ( 42 - 28 )( 42 - 26 )}} $$

$$⇒ {\sqrt{42 × 12 × 14 × 16 } } $$

$$⇒ {336 } $$

Area of △CDF = $ { 336} cm^2 $

Calculate the height of parallelogram ABCD

As parallelogram and triangle having same base and equal areas.

∴ Area of parallelogram = Area of triangle

⇒ Base x Corresponding height = 336

$$ { 28 × height = 336 } $$

$$ ⇒ { height = { 336 \over 28}} $$

$$ ⇒ { height = 12 } $$

Hence, the height of the parallelogram is 12 cm.

Question 5

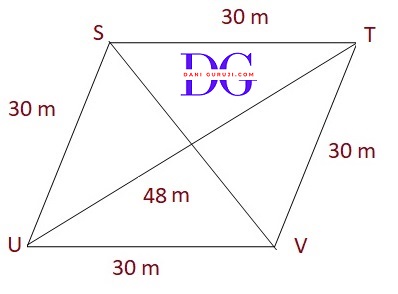
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?

Solution :

Draw a rhombus-shaped field first with the vertices as STUV. The diagonal SV divides the rhombus into two congruent triangles which are having equal areas.

Here, ST = TV = VU = US = 30 m and Diagonal SV = 48 m .

Consider the triangle TUV

First, calculate the semi-perimeter (s) of △TUV

Semi perimeter of the Triangle TUV (s) = $$ { { a + b + c } \over 2} $$

$$ { { 48 + 30 + 30 } \over 2} $$

$$ = 54m $$

Using Heron's formula calculate the area of Triangle TUV

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{54 ( 54 - 48 ) ( 54 - 30 )( 54 - 30 )}} $$

$$⇒ {\sqrt{54 × 6 × 24 × 24 } } $$

$$⇒ {432 } $$

Area of △TUV = $ { 432} m^2 $

Area of rhombus STUV

∴ Area of rhombus STUV = 2 x Area of triangle TUV

$$ { 2 × 432} $$

$$ ⇒ { 864} m^2$$

Number of cows = 18

Area of available grass field will each cow get = $$ { 864 \over 18} $$

Area of available grass field will each cow get = 48 $ m^2 $

Question 6

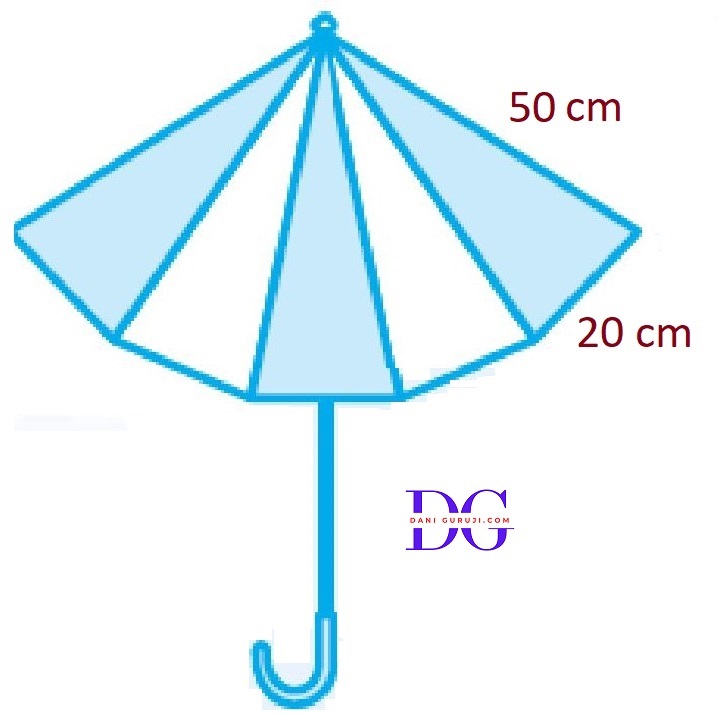
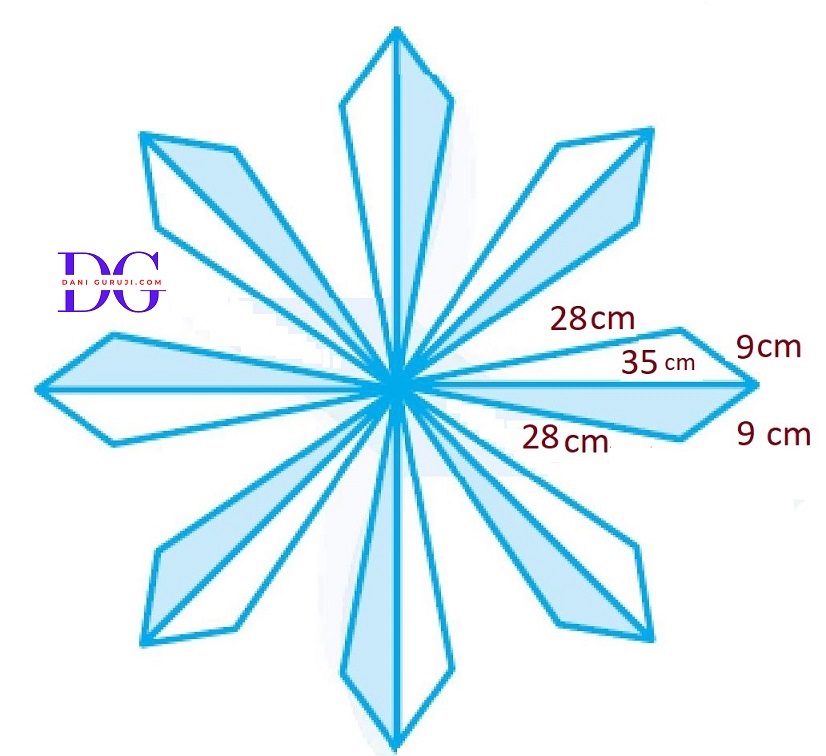
An umbrella is made by stitching 10 triangular pieces of cloth of two different colors (see Fig.), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each color is required for the umbrella?

Solution :

Given: Umbrella is made up of 10 triangular pieces of sides 50, 50 and 20 cm

First, calculate the Area of one Triangle

Semi perimeter of the Triangle (s) = $$ { { a + b + c } \over 2} $$

$$ { { 50 + 50 + 20 } \over 2} $$

$$ = 60m $$

Using Heron's formula calculate the area of Triangle

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{60 ( 60 - 50 ) ( 60 - 50 )( 60 - 20 )}} $$

$$⇒ {\sqrt{60 × 10 × 10 × 40 } } $$

$$⇒ {200 {\sqrt{6}} } $$

Area of of one Triangle = $ {200 {\sqrt{6}} }cm^2 $

According to question, there are 5 pieces of dark colour and 5 pieces of light colour.

Cloth required for 5 dark colour pieces =

$$ { 5 × {200 {\sqrt{6}} }} $$

$$ ⇒ { {1000 {\sqrt{6}} }} cm^2$$

Cloth required for 5 light colour pieces =

$$ { 5 × {200 {\sqrt{6}} }} $$

$$ ⇒ { {1000 {\sqrt{6}} }} cm^2$$

Question 7

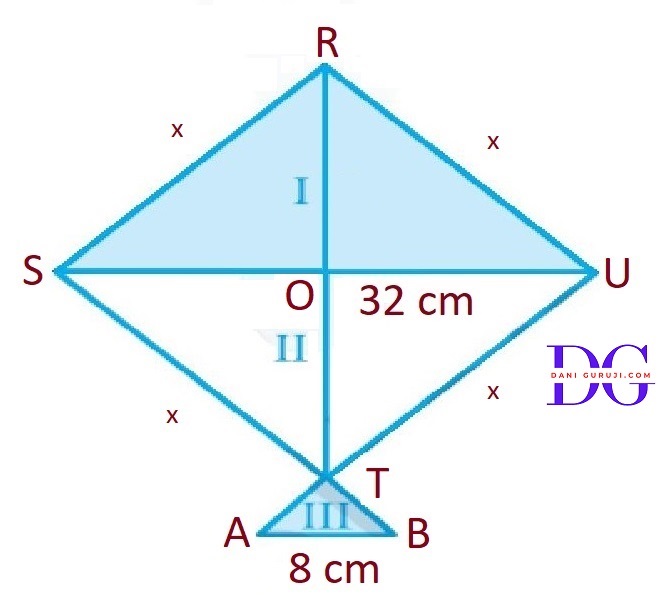
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in Fig. How much paper of each shade has been used in it?

Solution :

Given: Let kite RSTU is a square of side x cm and diagonals RT = SU = 32 cm

We know that diagonals of square bisect each other at right angle

then OS = 1/2 × SU

OS = 1/2 × 32 = 16 cm

OS = OU= 16 cm = OR = OT

Calculate the area of Part (I) and (II):

Since Part (I) and (II) are symmetrical, they have equal areas.

Triangles I and II are congruent right-angled triangles with base 32 cm and height 16 cm

The formula for the area of a right-angled triangle is:

Area of Part (I) △ = $ { 1 \over 2} $ × base × height

$$⇒ { { 1 \over 2} × 32 × 16 } $$

$$⇒ { 256 } cm^2 $$

Area of square = Area of two triangles ( I & II ) = $ 256 + 256 = 512cm^2 $

Calculate the area of Part (III) isosceles triangle ATB:

Semi perimeter of the Triangle (s) = $$ { { a + b + c } \over 2} $$

$$ { { 6 + 6 + 8 } \over 2} $$

$$ = 10m $$

Using Heron's formula calculate the area of Triangle

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{10 ( 10 - 6 ) ( 10 - 6 )( 10 - 8)}} $$

$$⇒ {\sqrt{10 × 4 × 4 × 2 } } $$

$$⇒ { 8 {\sqrt{5}} } $$

$$⇒ { 8 × 2.236 } $$

$$⇒ { 17.88 } $$

Area of shaded part III = $ {17.88 }cm^2 $

Question 8

A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Fig. ). Find the cost of polishing the tiles at the rate of 50 paise per $ cm^2 $

Solution :

Given 16 equal triangular tiles, here sides of a triangular shaped tile area 9 cm, 28 cm and 35 cm.

Calculate the area of the triangular shape :

Semi perimeter of the Triangle (s) = $$ { { a + b + c } \over 2} $$

$$ { { 28 + 9 + 35 } \over 2} $$

$$ = 36 cm$$

Using Heron's formula calculate the area of Triangle

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{36 ( 36 - 28 ) ( 36 - 9 )( 36 - 35)}} $$

$$⇒ {\sqrt{36 × 8 × 27 × 1 } } $$

$$⇒ {\sqrt{( 9 × 4 ) × ( 2 × 4 ) × ( 9 × 3 ) × 1 } } $$

$$⇒ { 36 {\sqrt{6}} } $$

$$⇒ { 36 × 2.45 } $$

$$⇒ { 88 .2} $$

Area of one triangular shape = $ {88 .2 }cm^2 $(Approx.)

Area of 16 triangular shape tiles

$$⇒ { 88 .2} × 16 $$

Area of 16 triangular tiles =$ { 1411.2} cm^2$ (Approx.)

Cost of polishing $ 1 cm^2 $ of the tiles = Rs. 0.50

Hence,

The total cost of polishing tiles = $ { 1411.2} × 0.50 $

= Rs. 705.60 (Approx.)

Question 9

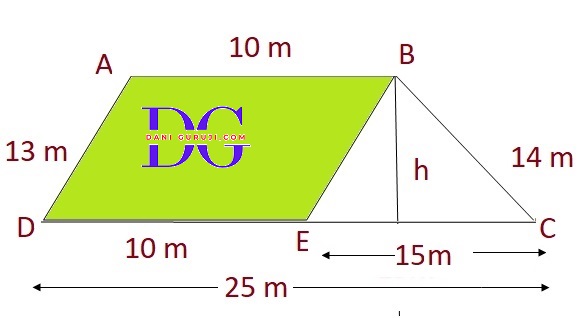
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m . The non-parallel sides are 14 m and 13 m . Find the area of the field.

Solution :

Given: field is in the form of a trapezium ABCD such that parallel side are AB = 25m and CD = 10m .

We can divide the trapezium into a parallelogram and a triangle by drawing a line from one vertex of the shorter parallel side (10 m) parallel to one of the non-parallel sides (say, the 13 m side).

The resulting triangle has sides equal to the two non-parallel sides and the difference between the parallel sides

The sides of this new triangle are: 13m, 15m, 14m

Calculate the area of the triangular shape BEC:

Semi perimeter of the Triangle BEC (s) = $$ { { a + b + c } \over 2} $$

$$ { { 13 + 14 + 15 } \over 2} $$

$$ = 21 m$$

Using Heron's formula calculate the area of Triangle BEC

$$ = {\sqrt{s( s−a)(s−b)(s−c)}} $$

$$ {\sqrt{21 ( 21 - 13 ) ( 21 - 14 )( 21 - 15)}} $$

$$⇒ {\sqrt{21 × 8 × 7 × 6 } } $$

$$⇒ {\sqrt{( 7 × 3 ) × ( 2 × 2 × 2 ) × ( 7 × 1 ) × ( 3 × 2 )} } $$

$$⇒ { 7 × 3 × 2 × 2 } $$

$$⇒ { 84 } $$

Area of Triangle BEC = $ {84 }m^2 $(Approx.)

Calculate the Height of the Trapezium :

The height of the trapezium is the same as the height of the triangle with respect to its base of 15 m.

We can use the standard area formula for a triangle: Area = $ { 1 \over 2}$ × base × height .

$$ 84 = { 1 \over 2} × 15 × height $$

$$ height = {{ {84 × 2} \over 15}} $$

$$ height = {{ {168} \over 15}} $$

$$ height = {11.2} m $$

Calculate the Area of the Trapezium:

Area of the trapezium = $ { 1 \over 2}$ × (sum of parallel sides) × height .

$$⇒ { 1 \over 2} × ( 25 + 10 ) × 11.2 $$

$$⇒ { 1 \over 2} × 35 × 11.2 $$

$$⇒ 17.5 × 11.2 $$

$$ ⇒ 196m $$

Hence, the area of field is 196 $ m^2 $