Surface Areas and Volume ⇒⇒ Exercise 12.2

Question 1

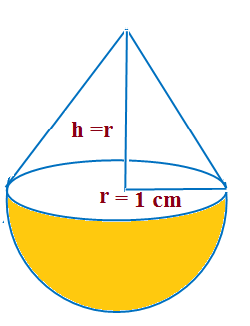
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π

Solution :

It is given that : Radius of cone, r = 1 cm.

Height of cone is equal to its radius

∴ h = r = 1cm.

It can be observed that the radius of the conical part and the hemispherical part is same

∴ Radius of the hemispherical portion, = 1 cm

To find the total volume of the solid, add the volume of the cone and the hemisphere.

Volume of solid = Volume of cone + Volume of hemisphere

( Volume of cone = ${{1 \over 3 }{\pi}r^2h }$ )

( Volume of hemisphere = ${{2 \over 3 }{\pi}r^3 }$ )

$$ = {{1 \over 3 }{\pi}r^2h } + {{2 \over 3 }{\pi}r^3 } $$

$$⇒ {{1 \over 3 }{\pi}(1)^2 × 1 } + [{{2 \over 3 }{\pi}(1)^3 }] $$

$$⇒ {{1 \over 3 }{\pi} } + {{2 \over 3 }{\pi} } $$

$$⇒ {\pi} ({1 \over 3 } + {2 \over 3 }) $$

$$⇒ {\pi} ({3 \over 3 } ) $$

$$⇒ {\pi} cm^3 $$

Hence, The volume of the solid is = ${\pi} $ cm³ .

Question 2

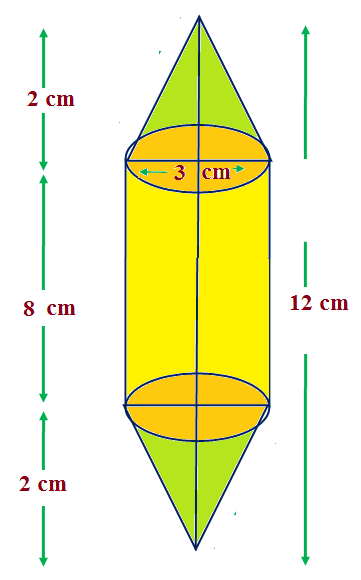
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)

Solution :

It is given that : diameter of conical part = 3 cm.

∴ Radius of the conical part , r = 3/2 cm

And Height of conical part h = 2 cm

The total length of the model is 12 cm. This includes the cylinder and the two cones.

Now, Height of cylindrical portion h₂ :

= Height of model - Height of 2 conical part

h₂ = 12 - 2 × 2 = 8 cm.

It can be observed that the radius of the conical part and the cylindrical portion is same

∴ Radius of the cylindrical portion, = 3/2 cm

Volume of air present in the model = Volume of cylinder portion + Volume of two conical ends.

( Volume of cone = ${{1 \over 3 }{\pi}r^2h }$ )

( Volume of cylinder = ${{\pi}r^2h_2 }$ )

$$ = {{\pi}r^2h_2 } + 2×{{1 \over 3 }{\pi}r^2h } $$

( Taking Common )

$$⇒ {{\pi}r^2 }×[ h_2+ 2×{{1 \over 3 }×h }] $$

$$⇒ {{\pi}({3 \over 2 })^2 } × [ 8 + 2 × {1 \over 3 } × 2 ] $$

$$⇒ {{\pi}×{9 \over 4 } } × [ 8 + {4 \over 3 }] $$

$$⇒ {{\pi}×{9 \over 4 } } × [ {{24 + 4 } \over 3 }] $$

$$⇒ {22 \over 7 }×{9 \over 4 } × {28 \over 3 } $$

$$⇒ {22 × 3} $$

$$⇒ {66} cm^3 $$

Hence, Volume of air present in the model = 66 cm³ .

Question 3

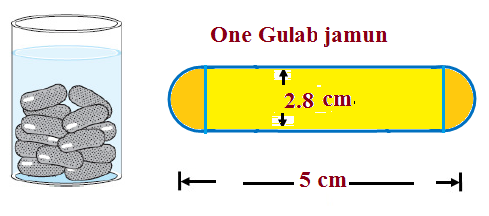
A gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see Figure).

Solution :

Lets first find volume of one gulabjamun

Volume of gulabjamun = Volume of cylinder + Volume of 2 hemisphere

It is given that : diameter of hemispherical part = 2.8 cm.

∴ Radius of the hemispherical part , $ r = 2.8/2 = 1.4 cm $

It can be observed that the radius of the cylindrical portion and the hemispherical part is same

∴ Radius of the cylindrical portion = 1.4 cm

Now, Length of cylindrical portion h :

= Length of gulabjamun - Length of 2 hemispherical part

$$= 5 - 2 × 1.4 $$

$$= 5 - 2.8 = 2.2 $$

Length of cylindrical portion , h = 2.2 cm

Now, Volume of one gulabjamun = Volume of cylinder + Volume of 2 hemisphere

( Volume of hemisphere = ${{2 \over 3 }{\pi}r^3 }$ )

( Volume of cylinder = ${{\pi}r^2h }$ )

$$ = {{\pi}r^2h } + 2×{{2 \over 3 }{\pi}r^3 } $$

( Taking Common )

$$⇒ {{\pi}r^2 }×[ h + 2×{{2 \over 3 }× r }] $$

$$⇒ {{\pi}(1.4 )^2 }×[ 2.2 + 2×{{2 \over 3 }× 1.4 }] $$

$$⇒ {{\pi}(1.4 )^2 }×[{{6.6 + 5.6} \over 3 }] $$

$$⇒ {{\pi}(1.4 )^2 }×[{{12.2} \over 3 }] $$

$$⇒ {{22 \over 7 }× 1.4 × 1.4}×{ 12.2 \over 3 } $$

$$⇒ {22 × 0.2 × 1.4}×{ 12.2 \over 3 } $$

$$⇒ { 75.152 \over 3 } $$

$$⇒ 25.05 cm^3 $$

Hence,Volume of one gulabjamun = 25.05 cm³

∴ Volume of 45 gulabjamun = $45 × 25.05$

= 1127.25 cm³

The volume of sugar syrup = 30% of the volume

$$⇒ 1127.25 × { 30 \over 100} $$

$$⇒ 338.17 cm^3 $$

The volume of sugar syrup = 338 cm³ (approx)

Question 4

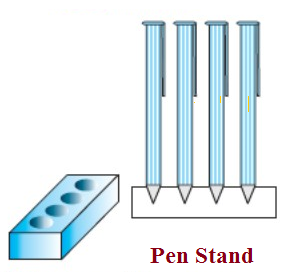
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand.(see Figure).

Solution :

Given : Dimensions of cuboid

Length = 15 cm , Width = 10 cm , Height = 3.5 cm

Radius of cone = 0.5 cm

And depth of cone = 1.4 cm

Since Cones are made inside the cuboid pen stand

Volume of wood in pen stand = Volume of cuboid – 4 × Volume of a conical depression.

( Volume of cone = ${{1 \over 3 }{\pi}r^2h }$ )

( Volume of cuboid = length × width × height )

$$ = ({l × b × h}) - 4 ×{{1 \over 3 }{\pi}r^2h } $$

$$⇒ {({15 × 10 × 3.5}) } $$

$$ - 4 ×{{1 \over 3 }{\pi}(0.5 )^2 ×1.4 } $$

$$ ({525}) - 4 ×{{1 \over 3 }×{22 \over 7 }× (.25 ) ×1.4 } $$

$$⇒ ({525}) - {{1 \over 3 }×{22 }× × 0.2 } $$

$$⇒ {525} - {4.4 \over 3 } $$

$$⇒ {525} - 1.47 $$

$$⇒ 523.53 cm^3 $$

The Volume of wood in pen stand = 523.53 cm³

Question 5

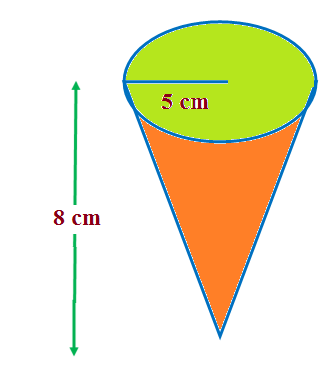
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.

Solution :

Given :

Radius of cone = r = 5 cm

And Height of cone = 8 cm

Radius of the lead shots = r₂ = 0.5 cm = 1/2 cm

When Lead Shots are dropped in the Vessel, the same amount of water will come out of the vessel as the Total Volume Of Lead Shots.

Hence, Volume of water flows out = 1/4 × Volume of Cone

Volume of cone = Volume of water in cone

Let us assume the number of Lead Shots to be n.

Thus the equation becomes :

= Volume of 'n' Lead Shots = 1/4 × Volume of Cone

( Volume of cone = ${{1 \over 3 }{\pi}r^2h }$ )

( Volume of sphere = ${{4 \over 3 }{\pi}(r_2)^3 }$ )

$$⇒ n ×[{{4 \over 3 }{\pi}(r_2)^3 }] $$

$$ = {1 \over 4 }×[{{1 \over 3 }{\pi}r^2h }] $$

( Substuting Values )

$⇒ n ×[{{4 \over 3 }{\pi}(0.5)^3 }] = {1 \over 4 }×[{{1 \over 3 }{\pi}(5)^2 × 8}] $

$⇒ n ×[{{4{\pi} \over 3 }(0.125) }] = {1 \over 4 }×[{{{\pi} \over 3 }(25) × 8}] $

$⇒ n ×{{0.5{\pi} \over 3 } } = {1 \over 4 }×{{200{\pi} \over 3 }} $

$⇒ n ×{{0.5{\pi} \over 3 } } = {50{\pi} \over 3 } $

$⇒ n = {50{\pi} \over 3 } × {3 \over {0.5{\pi} } } $

$⇒ n = 100 $

Hence, Total number of Lead Shots dropped in the vessel = 100

Question 6

A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm³ of iron has approximately 8g mass. (Use π = 3.14)

Solution :

It is given that : diameter of Larger cylinder = 24 cm.

∴ Radius of the Larger cylinder , r₁ = 24/2 cm = 12 cm.

Height of Larger cylinder , h₁ = = 220 cm

Now, Radius of the Smaller cylinder , r₂ = 8 cm.

Height of Smaller cylinder h₂ = 60 cm

Volume of pole = Volume of Larger cylinder + Volume of Smaller cylinder

( Volume of cylinder = ${{\pi}r^2h }$)

$$ [{{\pi}×(r_1)^2×(h_1) }] + [{{\pi}×(r_2)^2 ×(h_2) }] $$

$$ [{{\pi}×(12)^2 × 220 }] + [{{\pi}×(8)^2 ×60 }] $$

$$ {\pi} ×{[ (144 × 220 ) + (64 ×60 )]} $$

$$ ⇒ {\pi} ×{[ 31680+ 3840]} $$

$$ ⇒ { 35520 × 3.14} $$

$$ ⇒ 111532.8 cm^3 $$

Volume of pole = 111532.8 cm³

The mass of the pole can be found using the density of iron, which is given as 8g per 1 cm³

Mass of the pole :

= Density × volume

$ ⇒ 8 × 111532.8 $

$ ⇒ 892262.4 grams $

$ ⇒ 892.2624 kg $

Hence, approximately mass of pole = 892.2624 kg

Question 7

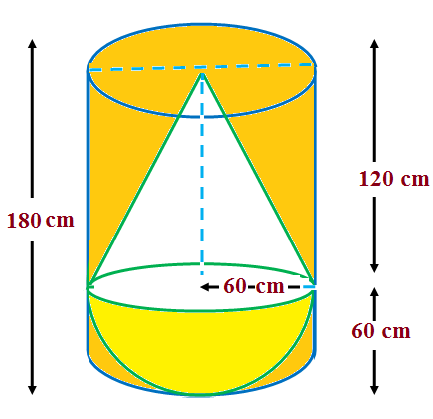
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.

Solution :

It is clear that : .

The volume of water (left) =Volume of a cylinder - Volume of solid

Given :

Radius of cone = 60 cm, height of cone = 120 cm.

Radius of hemisphere = 60 cm.

Radius of cylinder = 60 cm, height of cylinder = 180 cm.

Now ,Volume of hemisphere =

( Volume of hemisphere = ${{2 \over 3 }{\pi}r^3 }$ )

$$⇒ {{2 \over 3 }×{\pi}× (60)^3 } $$

$$⇒ {{2 \over 3 }×{\pi}× 60 × 60 × 60} $$

$$⇒ 144000{\pi}cm^3 $$

Now ,Volume of Cone =

( Volume of cone = ${{1 \over 3 }{\pi}r^2h }$ )

$$⇒ {{1 \over 3 }×{\pi}× (60)^2 ×120 } $$

$$⇒ {{1 \over 3 }×{\pi}× 60 × 60 × 120} $$

$$⇒ 144000{\pi}cm^3 $$

Volume of solid = Volume of hemisphere + Volume of Cone

$$⇒ 144000{\pi} + 144000{\pi} $$

$$⇒ 288000{\pi} cm^3 $$

Volume of solid = 288000${\pi} $ cm.³

Now, Volume of a cylinder can be calculated as follows:

( Volume of cylinder = ${{\pi}r^2h }$)

$$⇒ {{\pi}× (60)^2 × 180 } $$

$$⇒ {{\pi}× 60 × 60 × 180 } $$

$$⇒ { 648000{\pi}}cm^3 $$

Volume of a cylinder = 648000${\pi} $ cm.³

Now, The volume of water (left) =Volume of a cylinder - Volume of solid

$ = 648000 {\pi} - 288000 {\pi} $

$ = 360000 {\pi} $

$ = 360000 × {22 \over 7} $

$ = 1131428.57 cm^3 $

In Meter

= 1131428.57 × $({1 \over 100}m)$³

= 1131428.57 × ${1 \over 100}×{1 \over 100}×{1 \over 100} $m ³

= 1.13142857 m ³

Hence volume of water left in the cylinder is 1.13142857 m ³

Question 8

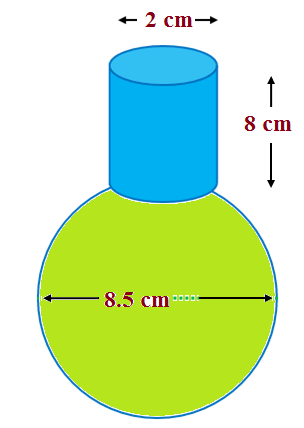
A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm³. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.

Solution :

It is given that : diameter of cylindrical portion = 2 cm.

∴ Radius of the cylindrical part , r = 2/2 cm = 1 cm.

Height of cylindrical part = 8 cm.

And diameter of sphere = 8.5 cm, ∴ r = 8.5/2 cm

Now, Volume of cylinder can be calculated as follows:

( Volume of cylinder = ${{\pi}r^2h }$)

$$⇒ {{\pi}× (1)^2 × 8 } $$

$$⇒ {{\pi}× 1 × 1 × 8 } $$

$$⇒ { 8{\pi}}cm^3 $$

Volume of cylinder = 8 ${\pi} $cm³

Now, Volume of sphere can be calculated as follows:

( Volume of sphere = ${{4 \over 3 }{\pi}r^3 }$)

$$⇒ {{{4 \over 3 }{\pi} }× ({8.5 \over 2 })^3} $$

$$ {{{4 \over 3 }{\pi} } × {8.5 \over 2 } × {8.5 \over 2 } × {8.5 \over 2 }} $$

$$⇒ {{{4 \over 3 }{\pi} } × { 76.77 } } $$

$$⇒ {{{\pi} } × {307.065 \over 3 }} $$

$$⇒ {102.354 }{\pi} cm^3 $$

Volume of sphere = 102.354 ${\pi} $cm³

Volume of spherical vessel = volume of cylinder + volume of sphere.

= 8 ${\pi} $ + 102.354 ${\pi} $

= 110.354 ${\pi} $

= 110.354 × 3.14

= 346.51 cm³

∴ answer find by the child is incorrect

Thus, volume of water vessel contains = 346.51 cm³